Introduction to derivative and its application

how do i solve Part 1 and Part 2? (attached in the file)

Introduction to derivative and its application

Derivatives are a fundamental tool of calculus. The purpose of this document is to informally introduce the derivative of a function and its application in optimization. We can utilize a computer system to find the derivative of a function. There are many programs that will do this tedious work for us and one of them is https://www.wolframalpha.com .

The derivative of a function  is the function denoted by  The derivative of a function at a point is the slope of the tangent line to the function, i.e., the slope of the tangent line of  at a point  is 

(source: wiki)

Example:

Find the tangent line to the function  at the point . First, we have to find the point which the tangent line passes through. The y-coordinate is , hence the point is . Second, we have to find the derivative . Using WolframAlpha: https://www.wolframalpha.com/input/?i=derivative+of+f%28x%29%3Dx%5E3-2x%2B1 we find the derivative . To find the slope of the tangent line we evaluate the derivative at ,  Using the point-slope formula we find the equation of the tangent line:

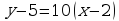
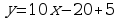
An application of derivative is to find the relative maximum and minimum of a function. To find the maximum or the minimum of a function, , we use the fact that the tangent line to the function is horizontal (the slope of the line is zero) at the points where the minimum or maximum is achieved.

To find the relative minimum or maximum of a function we first find the derivative, find all the points where the derivative is equal to zero and then we graph the function with its derivative. The relative minimum and maximum value(s) are always achieved at the points where the derivative is zero.

Example:

Find the relative minimum and maximum of the function .

We start by finding the derivative of  using WolframAlpha we get .

Now, we find the points where the derivative is zero, i.e., solve . We can also use WolframAlpha to get: . Using a graphing utility, we can find the graph of the function :

Relative maximum

Relative minimum

We see that the smaller out of the -values we found is a relative maximum and the larger point is a relative minimum, i.e., the relative maximum of the function is at the point  and the relative minimum is at the point .

Example:

Find the relative minimum and maximum of the function .

We start by finding the derivative of  using WolframAlpha and we get .

Now, we find the points where the derivative is zero. We can use WolframAlpha to get the following approximate values: . Using a graphing utility, we can find the graph of the function  and visually determine which of the solutions is a relative minimum and which is a relative maximum.

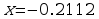
Relative minimum

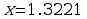
Relative maximum

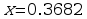
Relative maximum

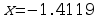
Relative minimum

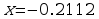
It seems that every year the price of Christmas trees increases and it peaks a week before Christmas Eve (December 17th). You contacted a tree grower from South Carolina and scored a good deal with him. He said the price per tree depends on the time of year you buy it. He agreed on the following formula for the price: , where  is the number of days before December 17th and  is the price per tree including transportation to your location. You estimate that the storage cost at your facility is going to be $0.56 per tree per day.

The two parts below are independent.

Part 1)

Let’s assume that you will sell all the trees for the same price on December 17th ().

• Create a function,  that represents your total cost for buying a tree and storing it until you sell it on December 17th (n=0) and graph the function.
• Find the relative minimum of this function using derivatives and show your work.
• What is the selling price per tree if you want to have 20% markup on cost?

Part 2)

It’s unlikely that you will sell all the trees on the same day but rather you will be selling them slowly and increase the price as Christmas approaches. Let’s assume that the final average selling price per tree you achieve if you will be selling it for  days before December 17th is 

• Graph the function  and explain why the graph looks like this.
• Assume that you have to pay for storing all the trees you buy and the cost is $0.56 per tree per day.
• Create a function,  that represents your profit per tree, i.e., the function is the difference of the average tree selling price and your total cost for buying a tree  days before December 17th and storing it.
• Use derivatives to find the maximum of  and determine when you should buy trees to sell.